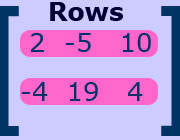
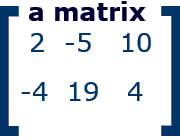Integrated Algebra II Page Links
Wednesday, September 29, 2010
Monday, September 27, 2010
Muliplying Matrices
Here Jordan Bayne explains the concept of dimension statement. I can really see he knows what is going on! Really nice!!!
[3 4] [1 2 3]
[5 6] [4 5 6]
[7 8]
The dimension statement for this would be 3X2 times 2X3.
- The numbers on the inside (in red) must be the same to carryout the multiplication process
- The numbers on the outside (in blue) tell what the dimension of the solution will be. In this particular problem, the solution will be a 3 X 3 matrix.
Tuesday, September 21, 2010
Int Algebra II - Erin Johnson: Can you multiply Matrices?
Good example of what I am looking for...click on the link!
INT ALG II - Alex Nguyen: Multiplying Matrices
To see what muliplying matrices are about...
INT ALG II - Alex Nguyen: Multiplying Matrices: "Scalar matrix multiplications Distribute the outside number for all the numbers on the inside. When multiplying matrices. We must note..."
INT ALG II - Alex Nguyen: Multiplying Matrices: "Scalar matrix multiplications Distribute the outside number for all the numbers on the inside. When multiplying matrices. We must note..."
Dimensions of a Matrix
Here is a good one from Alex Reid!!!
Dimensions of a Matrix: "The dimensions of a matrix refer to the number of rows and number columns of a given matrix.
The rows of a matrix are the numbers going horizontally.
The columns of a matrix are the numbers going vertically.
To find the dimensions of a matrix you must multiply the (number of rows x the number of columns). The dimensions for the matrix above would be (2 rows x 3 columns). The dimension of the matrix is 2 by 3 or (2x3).
Thursday, September 16, 2010
Dimensions of a Matrix
This looks like a good start! However, this student needs to add something about the square matrices and the matrix that is the identity matrix. These are important concepts that you need to be able to identify!
Dimensions of a Matrix: "To count matrices you count row X column
This matrix is one row by three columns, so it is a 1 x 3 matrix.
This matrix is three rows by three columns, so this is a 3 x 3 matrix.
This matrix is three rows by two columns, so it is a 3 x 2 matrix.
This is another three rows by three columns, so this is a 3 x 3 matrix.
 "
"
Dimensions of a Matrix: "To count matrices you count row X column
This matrix is one row by three columns, so it is a 1 x 3 matrix.
This matrix is three rows by three columns, so this is a 3 x 3 matrix.
This matrix is three rows by two columns, so it is a 3 x 2 matrix.
This is another three rows by three columns, so this is a 3 x 3 matrix.
Tuesday, September 14, 2010
Matrice multiplication
To multiply matrices you have to do ROW X COLUMN sum of the products.....
You will repeat this process several times...
Monday, September 13, 2010
We started matrices!
You will need these images to describe how to find the dimensions of a matrix.
Row X Column, identify the ones that are square and the identity matrix! Find the video on brightstorm, look on purplemath or any other math website to find other examples...use google images to see if you can find standing, price lists, anything that could be represented using matrices!!!
This picture is for fun....
These images you need for blogging!
 |
| Count the rows and columns, show how to identify the dimensions |
Wednesday, September 8, 2010
Tuesday, September 7, 2010
Types of Systems: GREAT!!!
Types of Systems:
 "
"
Case 1 | Case 2 | Case 3 |
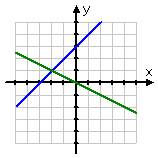 | 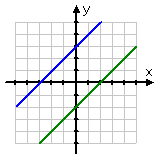 | 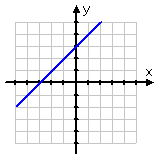 |
Independent system: one solution point | Case 2 | Case 3 |
 |  |  |
Independent system: one solution and one intersection point | Inconsistent system: no solution and no intersection point | Case 3 |
 |  |  |
Independent and consistent system: one solution and one intersection point | Inconsistent system: no solution and no intersection point | Dependent system: the solution is the whole line |
 |  |  |
Error Analysis - This one is perfect!
- For this particular problem the value of x is going up by 5, so the slope should be 10/5 or 2 and not 10/1. By inserting the points, the final equation should be solved. With this answer, y is not equal to 9+10x in the t-chart.
- In order for a particular point to be the solution to a system, it has to solve both equations. So in this case (1,-2) solves the first equation, but not the second equation of the system.
- For problem #22 the shading is correct, but the line should be a dotted line, not a soild line. For problem #23 the solid line is correct, but the shading should be above the line, not below it.
- For problem #20 the shading is correct, but the line should be a dotted line and not a solid line. For problem #21 the sloid line is correct, but the shading should be below the line, not above it.
Monday, September 6, 2010
Big week...here are all the assignments in Chapter 1
1) Quiz on writing equations
2) Quiz on systems
3) Quizstar - 3 Quizzes
4) Blogging - 3 Blogs
5) Chapter 1 Test
Extra credit packets - Misc. worksheets from the Chapter
This is how to work error analysis problems
The x's are going up by 5...not by 1. Therefore the slope would be 10/5...which equals 2 not 10/1.
Plus the final equation should be solved by plugging in the points, y is not equal to 9 + 10 * x in the t-chart!
Sunday, September 5, 2010
Friday, September 3, 2010
Thursday, September 2, 2010
Emailing to my blogs
Think I have figured out how to just email my blogs in...you can try it too! Goto to the Designs tab and the Settings, choose email or phone to update!
--
--
Robert Hill
(678)640-3180 Cell
(678)615-6274 Home
(770)564-1438 Work
Wednesday, September 1, 2010
Perpendicular Lines
This is an example from my Integrated Algebra I class....notice how I made corrections on their blog! Notice how they have a number for each line of the picture
1. Angle one is equal to angle
2. The lines are parallel
3. Angles 1 and 2 are set equal to 90
4. The lines angles are supplementary
Systems of Equations
Systems of Equations: "Consistent independent equations have one solution (x, y), which is where the two lines intersect. Consistent dependent equations have infinitely many solutions because they are the same line and inconsistent equations have no solution because they are parellel.
 I like this one...a good example of the different types of systems!
I like this one...a good example of the different types of systems!
y=a|x-h|+k
y=a|x-h|+k
the vertex on your graph will be (H,K)
the A tells you whether the V will open up or down,so if a is negative is will open down,and if it's positive, it will open up
Your A also tells you the slope,so if your a is 1 your slope would be 1/1 So up 1 over 1, up 1 over 1 etc.
the H moves the V right or left (opposite,so if you H is negative it would move right,and if it was positive it would move left)
the vertex on your graph will be (H,K)
the A tells you whether the V will open up or down,so if a is negative is will open down,and if it's positive, it will open up
Your A also tells you the slope,so if your a is 1 your slope would be 1/1 So up 1 over 1, up 1 over 1 etc.
the H moves the V right or left (opposite,so if you H is negative it would move right,and if it was positive it would move left)
Subscribe to:
Comments (Atom)