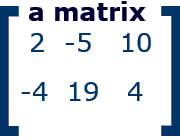The Teenage Brain

Muliplying Matrices

Here Jordan Bayne explains the concept of dimension statement. I can really see he knows what is going on! Really nice!!!

Muliplying Matrices: "Before you can begin to multiply matrices you need determine whether or not the matrices can be multiplied. To do that you must write a dimension statement.

[3 4] [1 2 3]
[5 6] [4 5 6]
[7 8]
The dimension statement for this would be 3X2 times 2X3.

• The numbers on the inside (in red) must be the same to carryout the multiplication process
• The numbers on the outside (in blue) tell what the dimension of the solution will be. In this particular problem, the solution will be a 3 X 3 matrix.

If the two matrices can be multiplied, you then multiply row X column and add the sum of the products to get the solution to the problem.

"

Int Algebra II - Erin Johnson: Can you multiply Matrices?

Good example of what I am looking for...click on the link!

Int Algebra II - Erin Johnson: Can you multiply Matrices?: "To determine whether or not matrices can be multiplied you first have to write a dimensions statement. Example of a dimensions statement: [..."

INT ALG II - Alex Nguyen: Multiplying Matrices

To see what muliplying matrices are about...


INT ALG II - Alex Nguyen: Multiplying Matrices: "Scalar matrix multiplications Distribute the outside number for all the numbers on the inside. When multiplying matrices. We must note..."

Dimensions of a Matrix

Here is a good one from Alex Reid!!!

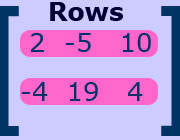
Dimensions of a Matrix: "

The dimensions of a matrix refer to the number of rows and number columns of a given matrix.

The rows of a matrix are the numbers going horizontally.

The columns of a matrix are the numbers going vertically.

To find the dimensions of a matrix you must multiply the (number of rows x the number of columns). The dimensions for the matrix above would be (2 rows x 3 columns). The dimension of the matrix is 2 by 3 or (2x3).

Dimensions of a Matrix

This looks like a good start!  However, this student needs to add something about the square matrices and the matrix that is the identity matrix.  These are important concepts that you need to be able to identify!

Dimensions of a Matrix: "To count matrices you count row X column

This matrix is one row by three columns, so it is a 1 x 3 matrix.

This matrix is three rows by three columns, so this is a 3 x 3 matrix.

This matrix is three rows by two columns, so it is a 3 x 2 matrix.

This is another three rows by three columns, so this is a 3 x 3 matrix.

"

Math is not linear on Prezi